MATE 3. Semana del 5 al 9 de Marzo del 2018.

MEDIDA.

• Análisis de las relaciones entre los ángulos agudos y los cocientes entre los lados de un triángulo rectángulo.

Les dejo el siguiente video para que construyan su clinómetro o goniómetro y la manera de medir  o calcular alturas  de edificios, árboles, etc. TAREA: Costruye tu goniómetro y llévalo el Martes a más tardar. Es OBLIGATORIO.  

1 Se conocen la hipotenusa y un cateto:

Ejemplo:

Resolver el triángulo conociendo:

a = 415 m y b = 280 m.

sen B = 280/415 = 0.6747     B = arc sen 0.6747 = 42° 25′

C = 90° - 42° 25′ = 47° 35′

c = a cos B   c = 415 · 0.7381 = 306. 31 m

2 Se conocen los dos catetos:

 

Ejemplo:

Resolver el triángulo conociendo:

b = 33 m y c = 21 m .

tg B = 33/21 = 1.5714      B = 57° 32′

C = 90° − 57° 32′ = 32° 28′

a = b/sen B   a = 33/0.8347 = 39.12 m

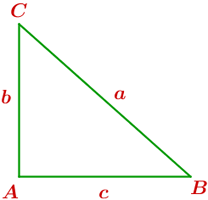
3 Se conocen la hipotenusa y un ángulo agudo:

 

Ejemplo:

Resolver el triángulo conociendo:

a = 45 m y B = 22°.

C = 90° - 22° = 68°

b = a sen 22°    b = 45 · 0.3746 = 16.85 m

c = a cos 22°     c = 45 · 0.9272 = 41.72 m

4 Se conocen un cateto y un ángulo agudo:

 

Ejemplo:

Resolver el triángulo conociendo:

b = 5.2 m y B = 37º

C = 90° - 37° = 53º

a = b/sen B     a = 5.2/0.6018 = 8.64 m

c = b · cotg B   c = 5.2 · 1.3270 = 6. 9 m

TAREA: PARA ENTREGAR EL VIERNES  9 DE MARZO.

$?$$C$$B$

Dado el siguiente triángulo rectángulo, calcula la medida de los lados y los ángulos desconocidos para cada caso:

1Dados b = 6 cm y c = 11 cm, calcula a, B y C.

  

  

  

2Dados b = 39 cm y B = 31º, calcula a, c y C.

  

  

  

3Dados c = 8 cm y B = 50º, calcula a, b y C.

  

  

  

4Dados a = 8 cm y C = 65º, calcula b, c y B.

  

  

  

Realiza: (Redondea a dos decimales en el caso que sea necesario)

5Calcula la altura de un árbol sabiendo que a una distancia de 8 metros se ve bajo un ángulo de 32º

Altura =  m

6Una escalera de 6 metros está apoyada sobre una pared y forma un ángulo de 53º con el suelo.

aCalcula la altura a la que se encuentra apoyada la escalera

Altura =  m

b¿Qué distancia hay desde el extremo inferior de la escalera hasta la pared?

Distancia =  m

7Halla la anchura del río, utilizando las medidas que se han tomado: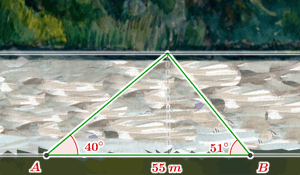 

Anchura =  m

Elige la opcion correcta:

8Dos personas separadas por una distancia de 5 km observan un avión con ángulos de 23º y 18º respectivamente. ¿A qué altura se encuentra el avión y quién se encuentra más cerca del avión?