MATE 3. Guía examen final

Guía examen final Mate 3

1.     Factoriza la SIGUIENTE EXPRESIÓN:

x2 - 1 = (x-1) (x+1)     

2.   Indica si las pendientes de las siguientes funciones son positivas o negativas:

                                             

1.   ¿Cuál es la razón trigonométrica tangente?

2.     ¿Cuál es la razón trigonométrica COSENO?

3.     Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada de la caja y no es reemplazada. Otra canica se saca de la caja. ¿Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?  R =

4.     Dos figuras semejantes tienen...

 a   el mismo tamaño y distinta forma.

 b   la misma forma y sus tamaños pueden ser proporcionales.

 c   el mismo tamaño y forma aunque pueden variar en determinadas ocasiones.

5.     Dada una figura cualquiera podemos construir otra semejante a ella...

a ampliándola, es decir "haciéndola más grande".

b reduciéndola, es decir "haciéndola más pequeña".

c Las dos respuestas anteriores son correctas.

Resuelve las siguientes ecuaciones

6.       x² - 5x + 6 = 0

R =  (x-3)(x-2) La solución es x1 = 3  y x2 = 2

7.     .    x² -x -20   

R =  (x+4)(x-5)   La solución es x1 = -4  y x2 = 5

8.     .  x² + 4x + 4

R = (x+2)(x+2)  La 

 solución es x1 = x2 = 2

9.     Se tienen cinco libros de distintas materias: Matemática, Biología, Química, Física y Lenguaje. Si se toma uno de ellos, ¿cuál es la probabilidad de que este sea de matemática o de física?

Solución:
Sean los eventos
A ≡Tomar el libro de Matemáticas.
B ≡Tomar el libro de Física.
La probabilidad pedida es:
P(A∪B) = P(A) + P(B) -P(A∩B)
Como A y B son eventos mutuamente excluyentes, P(A∩B) = 0.
Por lo tanto, la probabilidad pedida nos queda: 

   R = P(A∩B) = (1/5)+(1/5)-0= 2/5

10.  En una bolsa se tienen 3 bolitas verdes, 2 amarillas y 4 naranjas, ¿cuál es la probabilidad de que al sacar una bolita esta sea naranja o verde?
Solución:
Hay 4 bolitas naranjas y 3 verdes, esto es, 7 casos favorables a lo pedido. Aplicando la definición de Laplace: casos favorables 7
R =            P= casos favorables/ casos totales =7/9

11.  Averigua el valor de la variable dependiente en cada caso:

 Si y = (x + 4)²

a)    Cuando x = −6                         ENTONCES Respuesta    y = 4

b)    Cuando x = 6                                         ENTONCES  Respuesta         y = 100

12.  En una urna hay 3 fichas amarillas y 6 azules. ¿Cuál es la probabilidad de que, al sacar 2 fichas con reposición, éstas sean amarillas?

Respuesta

La probabilidad de sacar 1 ficha amarilla es de 3/9=>1/3, como existe reposición la 1ra extracción no afecta a la 2da extracción, por tanto, estamos frente a eventos independientes.

P(2 amarillas) = 1/3 * 1/3 = 1/9

13.  Resuelve la siguiente ecuación cuadrática por factorización

                                                                    R = (x-3) (x-2)

14.  Se lanza una moneda normal tres veces. ¿cuál es la probabilidad de sacar tres soles?

Respuesta

Como son eventos independientes, la probabilidad total es el producto de todas las probabilidades

P( 3 soles ) = P(S) * P(S) * P(S) = 1/2*1/2*1/2= 1/8

15.  Resolver gráficamente el siguiente sistema de ecuaciones:

                        

R =

 La solución del sistema es el punto donde las gráficas se cortan:

Un triángulo rectángulo  tiene como lados las siguientes expresiones:

cateto 1 : x

cateto 2 : x + 5

hipotenusa : 25

¿Con cuál de las siguientes ecuaciones puedes obtener la longitud de los catetos?

A) x² + 5x – 300 = 0

B) x² + 5x + 25 = 625

C) x² + 5x = 625

D) x ( x + 5)² = 625

1.     Resuelve la siguiente ecuación por factorización

             

R =   (x-2)(x-2) =  (x-2)²

1.     Un extraterrestre diminuto pero horrible está parado en la punta de la Torre Eiffel (que mide 324 metros de alto) y ¡amenaza con destruir la ciudad de París! Un agente de los Hombres de Negro está parado a nivel del piso, a 54 metros de distancia a la torre, y apunta su pistola láser al extraterrestre. ¿Con cuál función trigonométrica se puede calcular el ángulo al que el agente debe disparar su pistola? Descríbela.

tan = CO/CA = 324/ 54

1.     ¿Qué expresión algebraica permite calcular el número de canicas blancas de la enésima figura de esta sucesión?

    

a)    n² – n = 0

b)    n² – 2n = 0         

c)    n² + 2n = 0

1.      Encuentra la ecuación de la siguiente recta

1.                                                                y  = mx + b

                            m = 4/5   y    b = 4 entonces    la ecuación de la recta es    y = 4/5 + 4

23 ¿Cuál de las siguientes gráficas podrían representar la parábola dada por la ecuación cuadrática   2(x - 3)(x + 1)?

24. Escoge la gráfica a la que corresponde la siguiente función:    y = x² + x + 1

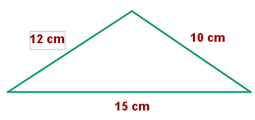
25. Razona si son semejantes los siguientes triángulos, en caso de ser afirmativa tu respuesta, indica por cuál criterio  lo son:

Sí son semejantes por el criterio LLL

26. La expresión  y = 2x, a qué gráfica se puede relacionar

                                                                                                                                                         

27. Completa la tabla de valores de la función lineal y = 3x

x	y
−3	−9
0
2

28. ¿Cuál de las siguientes ecuaciones cuadráticas es una parábola que abre hacia abajo?

1. 

2. 

          3. 

4. 

A) 1 y 3

B) 2 y 4

C) 3

D) 2

29. Se tiran dos dados. Encontrar la probabilidad de que la suma de las dos caras sea 1.

Probabilidad = 0

30. Los catetos de un triángulo rectángulo que miden 24 m y 10 m. ¿Cuánto medirán los catetos de un triángulo semejante al primero cuya hipotenusa mide 52 m?

                                              R =      b´= 48

                                                         c´ =20