MATE 3. Semana del 7 al 11 octubre 2019
EJE:
|
|
TEMA:
|
Proporcionalidad y
funciones
|
SUBTEMAS:
|
5. Dos maneras de
entender una variación cuadrática
|
CONTENIDO:
|
• Representación
tabular y algebraica de relaciones de variación cuadrática, identificadas en
diferentes situaciones y fenómenos de la física, la biología, la economía y
otras disciplinas.
|
INTENCIONES
DIDÁCTICAS:
|
Que los alumnos
relacionen dos conjuntos de datos que guardan una relación cuadrática e
identifiquen la expresión que modela dicha relación.
|
APRENDIZAJES
ESPERADOS
|
Analiza y compara diversos tipos de variación a partir de sus representaciones tabular, gráfica y algebraica, que resultan de modelar situaciones y fenómenos de la física y de otros contextos.
|
Las funciones cuadráticas son utilizadas en algunas disciplinas como, por ejemplo, Física, Economía, Biología, Arquitectura. Son útiles para describir movimientos con aceleración constante, trayectoria de proyectiles, ganancias y costos de empresas, variación de la población de una determinada especie que responde a este tipo de función, y obtener así información sin necesidad de recurrir a la experimentación.
Cuando se estudia cómo cambia un proceso, es conveniente encontrar un modo de representarlo matemáticamente. Para ello se puede considerar un recorte de la situación, identificar las variables que se relacionan, vincularlas de alguna manera (mediante expresiones matemáticas, tablas, gráficos, etc.) y utilizar diversos conocimientos matemáticos para analizar las relaciones que existen entre ellas y que son importantes para que el fenómeno se lleve a cabo. Algunos procesos se estudian a partir de las funciones cuadráticas, las cuales son un buen modelo para analizar situaciones en las cuales una de las variables en juego se relaciona con el cuadrado de la otra.
Los puntos del plano que verifican la ecuación y =ax2 + bx +c, con a distinto de 0 constituyen la gráfica.
En matemática, una función cuadrática es toda función que pueda escribirse de la forma:
f(x) =ax2 + bx +c
Donde a, b y c son números cualquiera, con la condición de que a sea un numero distinto de cero, x identifica una de las variables y f(x) es el valor que se obtiene para x a través de la función f. El punto (x; f(x)) pertenece al gráfico de la función.
En una función cuadrática: ax2 se denomina término cuadrático.
bx se denomina termino lineal.
c se denomina término independiente.
La gráfica de una función cuadrática es siempre una curva, o parte de una curva, que se llama parábola. Los puntos del plano que verifican la ecuación y =ax2 + bx +c, con a distinto de 0 constituyen la gráfica.
Aplicaciones de las Funciones Cuadráticas
Objetivo de Aprendizaje
· Aplicar ecuaciones cuadráticas a situaciones del mundo real para resolver problemas.
Introducción
Las funciones cuadráticas son más que curiosidades algebraicas — son ampliamente usadas en la ciencia, los negocios, y la ingeniería. La parábola con forma de U puede describir trayectorias de chorros de agua en una fuente y el botar de una pelota, o pueden ser incorporadas en estructuras como reflectores parabólicos que forman la base de los platos satelitales y faros de los carros. Las funciones cuadráticas ayudan a predecir ganancias y pérdidas en los negocios, graficar el curso de objetos en movimiento, y asistir en la determinación de valores mínimos y máximos. Muchos de los objetos que usamos hoy en día, desde los carros hasta los relojes, no existirían si alguien, en alguna parte, no hubiera aplicado funciones cuadráticas para su diseño.
Comúnmente usamos ecuaciones cuadráticas en situaciones donde dos cosas se multiplican juntas y ambas dependen de la misma variable. Por ejemplo, cuando trabajamos con un área. Si ambas dimensiones están escritas en términos de la misma variable, usamos una ecuación cuadrática. Porque la cantidad de un producto vendido normalmente depende del precio, a veces usamos una ecuación cuadrática para representar las ganancias como un producto del precio y de la cantidad vendida. Las ecuaciones cuadráticas también son usadas donde se trata con la gravedad, como por ejemplo la trayectoria de una pelota o la forma de los cables en un puente suspendido.
Usando la Parábola
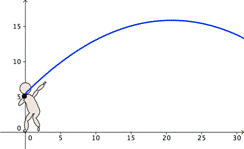
Una aplicación muy común y fácil de entender de una función cuadrática es la trayectoria seguida por objetos lanzados hacia arriba y con cierto ángulo. En estos casos, la parábola representa el camino de la pelota (o roca, o flecha, o lo que se haya lanzado). Si graficamos la distancia en el eje x y la altura en el eje y, la distancia que del lanzamiento será el valor de x cuando y es cero. Este valor es una de las raíces de una ecuación cuadrática, o intersecciones en x, de la parábola. Sabemos cómo encontrar las raíces de una ecuación cuadrática — ya sea factorizando, completando el cuadrado, o aplicando la fórmula cuadrática.
Problema
|
Un lanzador de peso puede ser modelado usando la ecuación
 , donde x es la distancia recorrida (en pies) y y es la altura (también en pies). ¿Qué tan largo es el tiro? | ||
2. A pesar de que el césped sintético del campo de un estadio es aparentemente plano, su superficie tiene la forma de una parábola. Esto es para que la lluvia resbale hacia los lados. Si tomamos la sección transversal del campo, la superficie puede ser modelada por
, donde x es la distancia desde la izquierda del campo y yes la altura del campo. ¿Cuál es el ancho del campo?
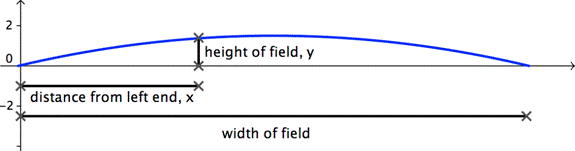
A) 80 pies
B) 1.5 pies
C) 234 pies
D) 160 pies R
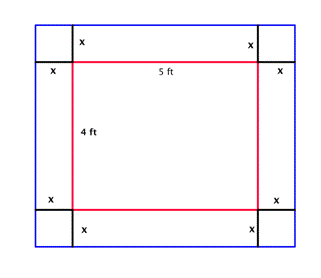
3. Bob hizo un edredón que mide 4 pies x 5 pies. Él tiene 10 pies cuadrados de tela para crear un borde alrededor del edredón. ¿Qué tan ancho debe hacer el borde para usar toda la tela? (El borde debe tener el mismo ancho en los cuatro lados.)
Escoge la función a la que corresponde cada una de las siguientes gráficas:
1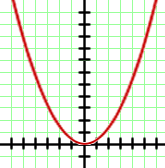
2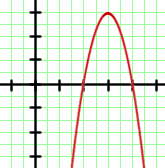
3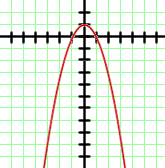
4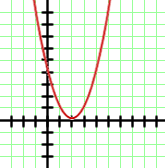
Escoge la gráfica a la que corresponde cada una de las siguientes funciones:
5y = x2 + x + 1
6y = 2x2 − x
7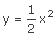
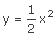
8y = −4x2 − 4x + 3
1. Un helicóptero dejó caer un
automóvil desde una altura de 245 metros . Algunos datos que se registraron son los siguientes:
Tiempo transcurrido
(seg)
|
0
|
1
|
2
|
3
|
4
|
Distancia de caída (m)
|
0
|
5
|
20
|
45
|
80
|
a) De acuerdo con la información, completen la siguiente tabla:
Tiempo
|
Distancia de caída
|
Altura a la que se encuentra el automóvil
|
0
|
0
|
245
|
1
|
5
|
240
|
2
|
20
|
|
3
|
45
|
|
4
|
80
|
|
5
|
||
6
|
||
7
|
a) ¿Cuánto tiempo tardó el
auto en llegar al suelo? ___________
b)
¿Cuál
de las siguientes expresiones permite calcular la distancia de caída (d) en función del tiempo transcurrido (t)? ________ Justifiquen su respuesta.
d = 5t d= 25t d= 5+t2
2. Cuando se proyecta una película, el área de la imagen depende de la distancia entre el proyector y la pantalla
Distancia
entre el proyector y la pantalla (m)
|
1
|
2
|
3
|
Área de la
imagen en m2
|
4
|
16
|
36
|
a) Escriban la expresión algebraica que muestre la relación entre las distancias y
las áreas. ________________________
b)
Anoten
los datos que hacen falta en la siguiente tabla.
Distancia entre el proyector y la pantalla
(m)
|
1.5
|
2.5
|
3.5
|
4.5
|
Área de la imagen (m2)
|
c)
Utilicen
la expresión anterior para encontrar a qué distancia se debe colocar el
proyector de manera que el área de la imagen sea de 24.01 m2 .
d
= ______________
3.
Se
tiene un cuadrado que tiene por lado x cm, ¿cuál es la expresión algebraica
que permite determinar el área (y)? _____________________ Si al cuadrado se le
aumentan 2 cm en una de las dimensiones y 3 cm en la otra dimensión, ¿cuál es
la expresión que determina el área (y) del rectángulo que se ha formado?
___________________________________________
4.
En
la escuela se organizó un torneo de Voleibol. Antes de iniciar un partido entre
dos equipos de 10 integrantes cada uno, los jugadores de cada equipo saludarán
a todos los elementos del equipo contrario.
a)
¿Cuántos saludos se realizan en total? ____________________________________
b).
Si uno de los equipos tiene nueve integrantes, ¿cuántos saludos se realizarán
en total? ________________________________________
c)
¿Qué expresión algebraica permite obtener el total de saludos (y), si uno de
los equipos tiene x cantidad de integrantes y otro tiene un jugador menos?
_________________________
5.
Se
tiene un rectángulo que tiene un perímetro de 20 metros, el cual tiene un lado
de longitud x metros. Escriban una expresión algebraica que represente la
variación del área (y) en función de x.
________________________________________________________
